Este problema matemático de empilhamento de blocos tem uma solução absurda que você precisa ver para acreditar
Em princípio, essa matemática impossível permite uma ponte sem cola de blocos empilhados que podem se estender pelo Grand Canyon-e ao infinito
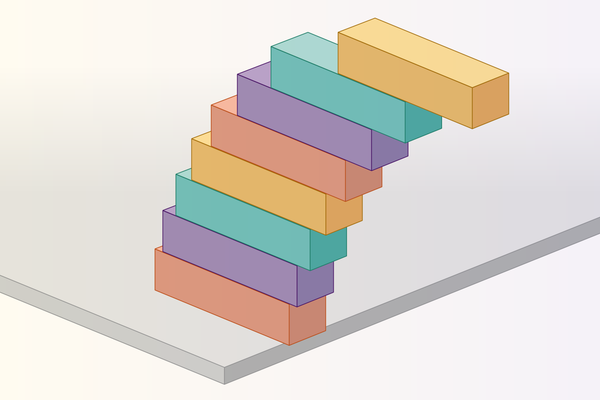
Aqui está um experimento alucinante que você pode experimentar em casa: junte alguns blocos infantis e coloque-os em uma mesa. Pegue um quarteirão e empurre -o lentamente sobre a borda da mesa, polegada por polegada, até que esteja à beira de cair. Se você possui paciência e uma mão firme, poderá equilibrá -la para que exatamente metade dele pegue a borda. Cutuque -o mais longe, e a gravidade vence. Agora pegue dois quarteirões e comece de novo. Empilhando um em cima do outro, até onde você pode chegar ao final do bloco superior para cutucar a borda da mesa?
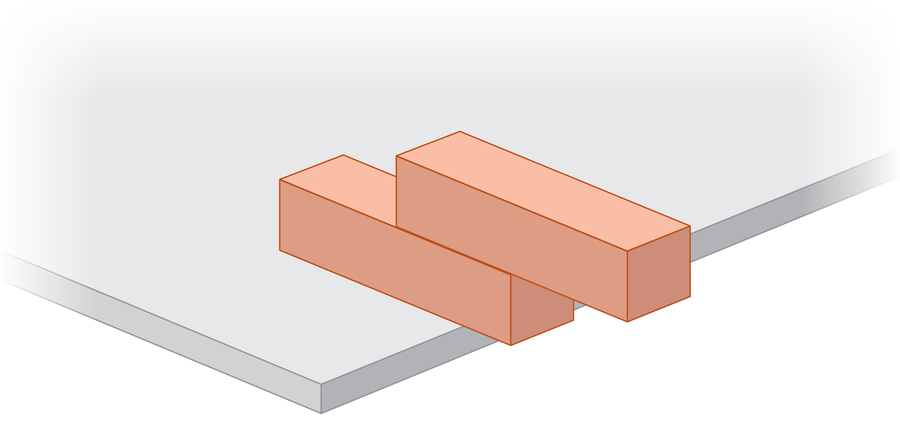
Continue. Empilhando o maior número possível de blocos, qual é a mais longa saliência que você pode alcançar antes de toda a estrutura de derrubar? É possível que a torre estenda um comprimento total do bloco além do lábio da tabela? A física permite dois comprimentos de bloco? A resposta impressionante é que a ponte empilhada pode se esticar para sempre. Em princípio, uma pilha independente de blocos pode abranger o Grand Canyon, não é necessária cola.
Sobre apoiar o jornalismo científico
Se você está gostando deste artigo, considere apoiar nosso jornalismo premiado por assinando. Ao comprar uma assinatura, você está ajudando a garantir o futuro das histórias impactantes sobre as descobertas e idéias que moldam nosso mundo hoje.
Não clique em “Checkout” em um pacote infinito de blocos Jenga ainda. Os práticos do mundo real, como formas irregulares de blocos, correntes de ar e o peso esmagador de um edifício sem fim, podem dificultar suas aspirações de engenharia. Ainda assim, entender por que a saliência não tem limite em um mundo matemático ideal é esclarecedor. A explicação depende da série harmônica da matemática e do conceito de física do centro de massa, duas idéias aparentemente simples com poder enorme. (Para mais diversão, confira: Qual a altura que você pode construir uma torre sem ela derrubar?)
Sua intuição pode dizer que um único bloco pode pendurar metade da massa além da borda da mesa antes de dar gorjeta. Mas por que é isso? Todo objeto tem um centro de massa – um ponto único em que podemos imaginar o peso de todo o objeto a ser concentrado quando estamos pensando em equilíbrio. Enquanto o centro de massa estiver acima da tabela, o objeto permanece colocado. No momento em que o centro de massa passa por uma vantagem, no entanto, a gravidade puxará tudo. No caso de uma colher, um item com distribuição irregular de peso, podemos pendurar mais da metade da alça do utensílio sobre uma borda antes de dar as pontas, porque o centro de massa está mais perto de sua cabeça, onde reside mais peso. Para a nossa ponte empilhada, assumimos que nossos blocos são todos idênticos, com uma densidade uniforme (ou seja, eles não são mais densos em algumas partes do que outras); portanto, o centro de massa de cada um fica no ponto médio.
Quando adicionamos mais blocos, devemos explicar o centro de massa de toda a torre. Considere o caso de dois blocos. Sabemos que o bloco superior pode estender metade de sua massa além da que ele abaixo dele. Mas depois de fazer isso, até onde podemos empurrar o bloco inferior?
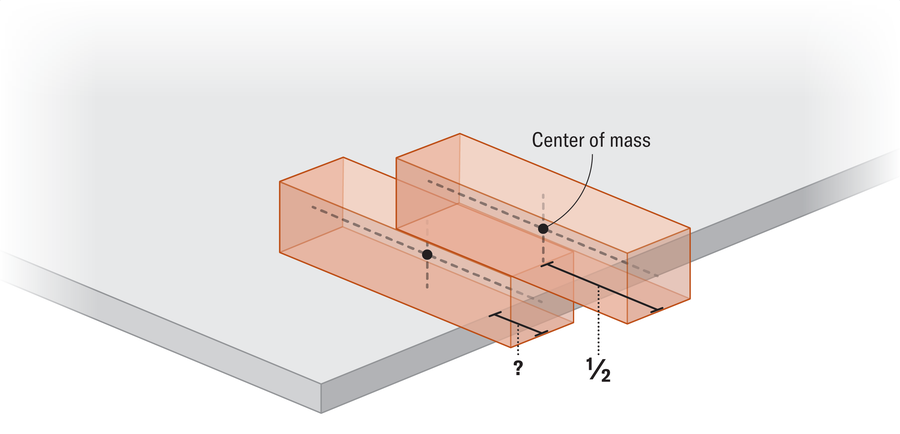
Por simplicidade, digamos que cada bloco tenha um comprimento de 1 e uma massa de 1. Você descobrirá que o bloco inferior pode cutucar apenas um quarto do caminho (em comparação com a metade do seu comprimento na borda quando estava sozinho). Nesse ponto, o centro de massa do bloco superior e o centro de massa do bloco inferior são equidistantes da borda da tabela (o centro de massa do bloco superior fica um quarto à direita da borda, e o centro de massa do bloco inferior fica um quarto à esquerda da borda). Então o combinado centro de massa do sistema de dois blocos repousa perfeitamente equilibrada acima da borda da tabela.
Um padrão surge à medida que continuamos a adicionar blocos à estrutura. O bloco superior se estende 1⁄2 Além do abaixo, o segundo bloco se estende 1⁄4 Além do bloco abaixo dele, o terceiro se estende 1⁄6o quarto se estende 1⁄8então os blocos subsequentes se estendem 1⁄10Assim, 1⁄12e assim por diante. Para ver o porquê, vamos olhar para outro exemplo. Suponha que tenhamos uma torre estável que contenha cinco blocos, e queremos adicionar um sexto bloco abaixo dela e depois deslizar toda a estrutura para fora, o máximo possível. É útil conceituar essa imagem como apenas dois blocos: um com uma massa de 5 no topo de um único bloco com uma massa de 1. Primeiro seguiremos o bloco pesado, até onde será que seu centro de massa fica logo acima da borda do bloco inferior. Podemos então empurrar o bloco inferior exatamente 1⁄12 de uma unidade além da borda da mesa. Como sabemos disso?
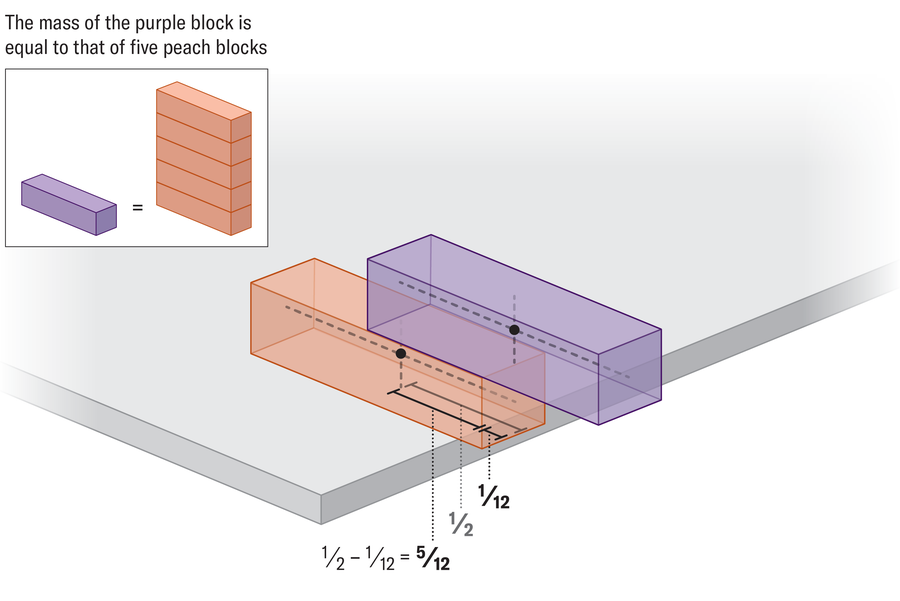
Novamente, a resposta se resume a equilibrar os centros de massa dos dois blocos, só que desta vez, porque o bloco inferior é cinco vezes mais leve, seu centro de massa deve acabar cinco vezes mais longe na mesa para neutralizar o peso do bloco mais pesado. Isso é conhecido como a lei da alavanca – pense em como um livro parece mais pesado na palma da mão, quanto mais você a afasta do seu corpo; portanto, uma brochura em um braço totalmente prolongada pode parecer equivalente a um livro mantido próximo ao seu torso. A distância entre o centro da massa do bloco superior e a borda da mesa é 1⁄12e a distância para o bloco inferior é 1⁄2 – 1⁄12 = 5⁄12ou cinco vezes mais. Um cálculo semelhante revela a saliência correta em todos os níveis da torre.
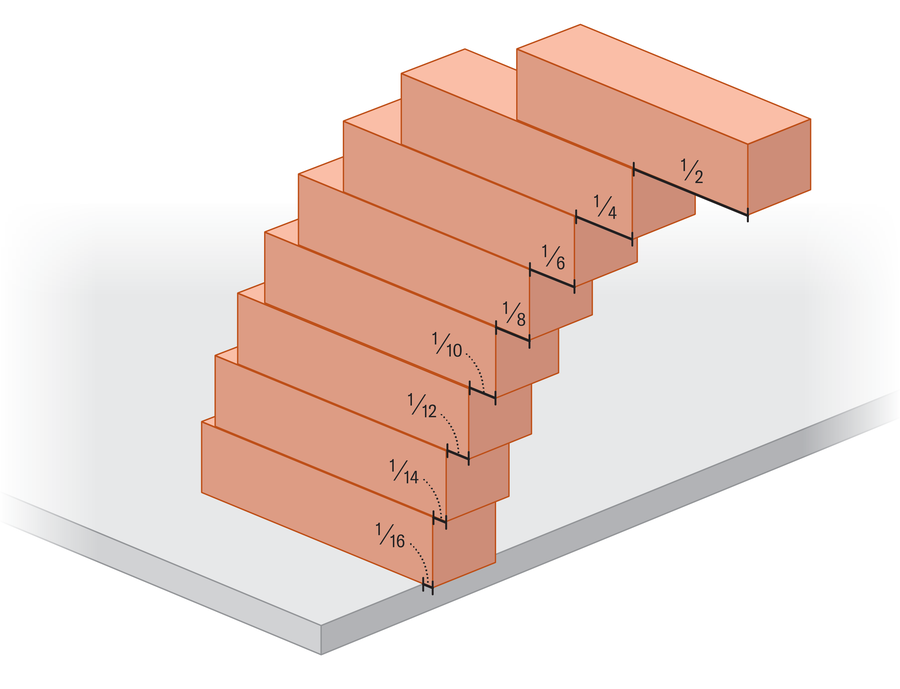
Respondendo à nossa pergunta de abertura (a que distância a torre pode se estender?) Equivale a somar todas essas saliências sucessivas. Se você tiver 10 blocos, eles podem se estender a 1⁄2 + 1⁄4 + 1⁄6 + 1⁄8 + 1⁄10 + 1⁄12 + 1⁄14 + 1⁄16 + 1⁄18 + 1⁄20o que soma cerca de 1,464 comprimentos de bloco além da borda. Mas qual é o limite para até onde podemos empilhar blocos? Para isso, devemos adicionar infinitamente muitos desses termos cada vez maiores. O padrão resultante tem uma semelhança impressionante com uma das somas infinitas mais famosas da matemática, a série harmônica, que leva o recíproco de cada número de contagem (ou seja, 1 dividido por todo número inteiro positivo) e resume todos eles:
1 + 1⁄2 + 1⁄3 + 1⁄4 + 1⁄5 + …, e assim por diante.
Se você olhar de perto, poderá notar que as saliências do problema de empilhamento de blocos são exatamente metade de cada um desses termos: 1⁄2 + 1⁄4 + 1⁄6 + 1⁄8 + 1⁄10 + …
O cálculo, o ramo da matemática que se aproxima de como as coisas mudam, ensina -nos que, mesmo ao adicionar infinitamente muitos termos que diminuem, às vezes a soma converge para um valor finito e às vezes diverge para o infinito. O total da série harmônica cresce incrivelmente lentamente. Os primeiros 100.000 termos somam cerca de 12,1, enquanto os primeiros milhões de termos são iguais apenas a 14,4. Ainda assim, no ritmo do caracol implacável, a série harmônica cresce para sempre.
Cada operação individual no problema de empilhamento de blocos é igual a metade de um termo na série harmônica. Como metade do infinito ainda é o infinito, a saliência potencial da torre também não tem limites.
Obviamente, a tradução de matemática pura em prática sempre vem com obstáculos, mas o problema de empilhamento de blocos oferece um desafio de destreza divertido. Com apenas quatro blocos, você poderá estender o top um por um comprimento total após a borda (1⁄2 + 1⁄4 + 1⁄6 + 1⁄8 = ~ 1.042). Para cumprir minha due diligence jornalística, tentei isso em casa com cartas de jogo na minha mesa de café. Depois de alguns minutos de mexer no paciente, consegui equilibrar o cartão superior logo depois da borda, com ele pendurado inteiramente fora da mesa e me senti como um mágico.
Dois comprimentos de bloco total além de qualquer superfície exigiriam 31 peças. Enquanto isso, 100 milhões de peças nem sequer lhe dariam 10 comprimentos completos de saliência, porque a soma dos primeiros 100 milhões de termos da série harmônica, todos divididos por 2, é igual a cerca de 9,5. Portanto, será necessário um pouco de coragem para abranger o Grand Canyon. Em grandes escalas, a física entra em ação para derrubar a diversão dos matemáticos. Mas em condições idealizadas em que o centro de massa e a série harmônica apenas governam o poleiro, as possibilidades são literalmente infinitas.