Memória do flash subnanossegund

Fabricação de dispositivos

Os portões de controle inferior (5/15 nm Cr/Au) foram padronizados por litografia por feixe E com um processo fotorresista de bicamada seguido pela deposição de metal pela evaporação do feixe E em dióxido de silício (300 nm)/substratos de silício. Para a memória flash, seguindo a preparação dos portões inferiores, um Al₂O₃ Óxido de bloqueio e um HFO₂ A camada de armadilha foi cultivada por deposição de camada atômica térmica a 250 ° C. Durante o processo de deposição da camada atômica, trimetilalumuminio e tetrakis (etilmetilamino) hafnium reagiram com água para formar Al₂O₃ e HFO₂respectivamente. Esse processo de deposição da camada atômica é necessária apenas para a fabricação de flash. Wse₂os cristais de grafeno e HBN foram adquiridos do HQ grafeno e a heteroestrutura dos materiais 2D foi preparada usando esfoliação mecânica e uma abordagem de transferência a seco. O floco HBN foi transferido pela primeira vez para o portão inferior e, em seguida, o material de corpo fino foi transferido para o floco HBN. A adesão da heteroestrutura no substrato foi melhorada pelo recozimento de calor por mais de 2 h a 200 ° C sob uma atmosfera de nitrogênio. Em seguida, os contatos de drenagem-fonte foram padronizados pela litografia de feixe eletrônico e uma pilha de metal (WSE₂10/12 nm sb/pt; grafeno, pilha de 5/60 nm Cr/Au) foi depositado usando a evaporação do feixe eletrônico. Após a abordagem padrão de elevação, os dispositivos com o contato SB/PT foram recozidos pela placa quente na caixa de luvas (200 ° C, 2 h) para formar a liga. Para conduzir o teste de memória flash sub-1-NS, os fios e almofadas de metal combinados com as sondas de radiofrequência foram padronizados pela litografia do feixe eletrônico e o Cr/Au de 5/60 nm foi depositado por evaporação do feixe eletrônico.

Caracterização do material

A microscopia de força atômica para os dispositivos foi medida por um sistema MFP-3D Origin+ (Asylum Research, Oxford Instruments). A amostra pronta para microscopia de transmissão-elétron foi preparada usando uma técnica de elevação de vigas de íons focada in situ em um Thermo Scientific Helios Eurofins EAG LAB G4 HX ou UC Microscópio eletrônico com feixe de íons/varredura de feixe duplo UC. A amostra foi plaqueada com Iridium e tapada com Pt de feixe de elétrons e Pt de feixe de íons antes de fresar. A imagem da microscopia eletrônica de transmissão foi capturada com um microscópio eletrônico de transmissão Tecnai F20 Tecnai F20 operado com uma tensão de aceleração de 200 kV. A espectroscopia-dispersiva de energia foi realizada no sistema Super X FEI no modo de microscopia eletrônica de transmissão de varredura.

Medições elétricas

Neste trabalho, os dispositivos foram medidos à temperatura ambiente e sob condições atmosféricas em uma estação de sonda (MPI, TS200-SE). A verificação do mecanismo 2D-HCI sob várias temperaturas foi realizada usando uma estação de sonda de baixa temperatura em terra em terra em terra sob um vácuo de <10^-4mbar. Os sinais CC foram gerados usando uma unidade de medida de origem (B1500A, Keysight). Os pulsos de tensão (≥20 ns) foram gerados usando uma unidade de gerador de pulso semicondutores (B1500A, Keysight). A medição sub-1-NS foi realizada com base em nosso sistema caseiro de alta velocidade (Fig. 19). As formas de onda do pulso de tensão foram capturadas pelo osciloscópio (DPO 5204, Tektronix). O teste elétrico foi realizado usando um analisador de parâmetro de dispositivo semicondutor (B1500A, Keysight).

Derivação teórica do modelo quase-2D

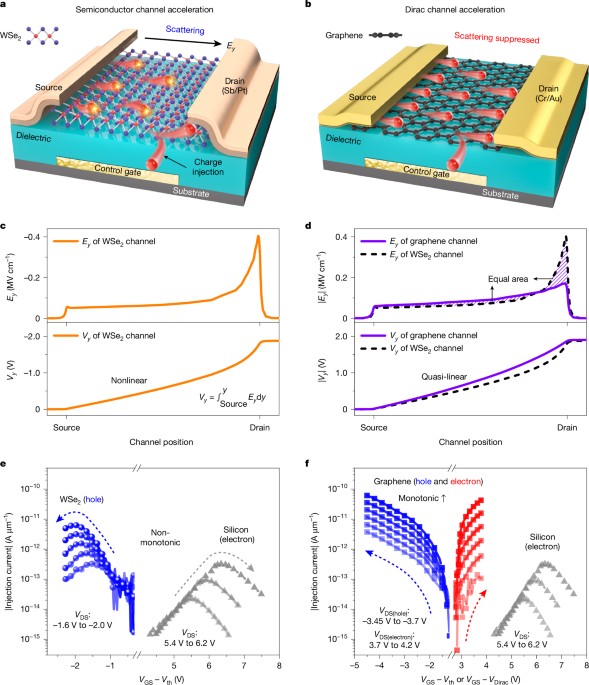
Empregamos um modelo quase-2D com a mesma estrutura que nosso transistor 2D fabricado para análise. O x a direção é definida como a superfície do canal para gabar verticalmente, e o y a direção é definida como fonte para drenar horizontalmente, onde o ponto zero do x e y Os eixos são a superfície do canal e a fonte, respectivamente. y₀ está na borda principal da região de saturação da velocidade, V(y) é o potencial horizontal no canal, t_cap é a espessura do canal, E_x e E_y são o campo elétrico vertical e horizontal no canal, E_dielétrico é o campo elétrico vertical no dielétrico e E_sentado e V_Dssat são os E_y e V(y) na borda principal da região de saturação da velocidade, respectivamente. Para obter o E_y Distribuição, é necessário resolver a equação de Poisson e a equação de transporte atual simultaneamente na região de saturação da velocidade. É expresso como

onde ρ(xAssim, y) é a carga fechada na caixa gaussiana, ε₀ é a permissividade a vácuo eε_cap é a permissividade relativa do canal. Sob as condições de (1) o corpo fino ( t_cap → 0) do canal de material 2D resulta em uma região de pinça quadrada, indicada como uma caixa gaussiana, (2) E_y apenas varia com a posição horizontal e (3) o valor de E_x no x= 0 está próximo de zero, o que nos permite substituir \ (\ frac {\ parcial {e} _ {x}} {\ parcial x} \) com o valor médio dado por \ (\ frac {{e} _ {x} ({t} _ {{\ rm {ch}}}, y)} {{t} _ {{\ rm {ch}}}} \)Aplicamos a lei de Gauss

onde E_dielétrico é o campo elétrico no portão dielétrico e ε_dielétricoé a permissividade relativa dielétrica. Equação diferenciadora (5) em relação a ynós temos

Nós podemos expressarE_dielétrico( t_cap Assim, y) como

onde V_Gs é o viés do portão -fonte, V_Fb é a tensão de banda plana, φ_B é o potencial da superfície et_dielétricoé a espessura dielétrica. Como as condições de contorno na borda principal da caixa gaussiana: V (y=y₀ ) =V_DssateE_dielétrico( y= y₀) = (V_Gs– V_Fb– 2φ_B– V_Dssat)/t_dielétricopodemos obter isso \ (\ rho (x, y) = \ frac {{\ varepsilon} _ {0} {\ varepsilon } _ {{\ rm {dielectric}}}} {{t} _ {{\ rm {ch}}} {t} _ {{\ rm {diel ectric}}}} ({v} _ {{\ rm {gs}}}-{v} _ {{\ rm {fb}}}-2 {\ varphi } _ {{\ rm {b}}}-{v} _ {{\ rm {dssat}}}) \). Então a equação (6) é simplificada para

onde λé o comprimento efetivo da caixa gaussiana, também conhecida como comprimento da escala. Aplicando as condições de contorno na borda principal da caixa gaussiana:V(y = y₀ ) = V_Dssat eE_y(y=y₀) =E_sentadopodemos escrever oV(y) eE_y(y) na caixa gaussiana como

e

Na extremidade do dreno do canal onde o campo atinge o pico

e

onde δLé a região que se estende do ponto de pit-off do canal para o ralo. As equações (11) e (12) podem ser combinadas para produzir

e

Esta equação mostra que oE_ymáxé altamente sensível at_capescala.