Quão lógico você é? Teste suas habilidades com esses problemas do novo International Logic Olympiad
Em apenas seu segundo ano, a Olimpíada Internacional de Lógica já está crescendo à medida que a lógica se torna cada vez mais crucial em nosso mundo em constante mudança

No início deste mês, 36 estudantes do ensino médio de todo o mundo de todo o mundo pisaram no campus quente e arejado da Universidade de Stanford. Dos mais de 4.000 estudantes de mais de 2.000 escolas em mais de 90 países diferentes, essas 36 pessoas foram selecionadas para competir como finalistas da segunda Olimpíada Lógica Internacional (OIT).
A competição incluiu três rodadas de testes, culminando na última em Stanford. Lá equipes de dois a quatro se engajaram em uma batalha de inteligência, resolvendo parentes lógicos e competindo em jogos matemáticos contra o cenário dos sopéns de Palo Alto, Califórnia. Os vencedores deste ano foram os alunos da 11ª série, que estão de acordo com o time de time, que é um time, que é o que é o time de time, que é um dos vencedores da 11ª série, que é o que é um time de time de time, que é um time de térmico, que é um dos vencedores da 11ª série, que é o que é um time de térmico, que é um time de térmico, que é o que é um time de término, que é um dos vencedores da 11ª série, que é o que é o que é um time, que é o que é um dos vencedores, depois de um térmico. Skit de vídeo que eles assistiram durante uma sessão de revisão. A chave para o sucesso deles, eles afirmam, foi muita prática e trabalho em equipe. “Acho que parte da razão pela qual fomos capazes de nos sair tão bem, porque eu conheço meus companheiros de equipe muito bem e somos amigos há muitos anos”, diz Song.
A OIT foi lançada pelo cientista da computação e lógico de Stanford Michael Genesereth em uma colaboração entre a Universidade e a organização sem fins lucrativos Luminas. “Usamos a lógica em quase tudo o que fazemos”, diz Genesereth. Os médicos empregam lógica para diagnosticar pacientes, os advogados usam argumentos lógicos no tribunal, e a lógica é mais essencial do que nunca para avaliar o mundo em rápida mudança ao nosso redor, observa ele. “Nem tudo tem a ver com matemática e fórmulas e álgebra”, acrescenta Genesereth.
Sobre apoiar o jornalismo científico
Se você está gostando deste artigo, considere apoiar nosso jornalismo premiado por assinando. Ao comprar uma assinatura, você está ajudando a garantir o futuro das histórias impactantes sobre as descobertas e idéias que moldam nosso mundo hoje.
A maioria dos vencedores deste ano tem interesse em ciência da computação, juntamente com a ciência ambiental, a matemática aplicada e a engenharia elétrica, mas Zhang diz que nem a matemática nem a ciência da computação são seu “terno forte” e que ele planeja entrar em ciências políticas. “Muitos dos problemas exigem soluções de pensamento e criativos muito expansivas, e acho que isso definitivamente me ajudará se eu entrar em políticas no futuro”, explica ele.
Um aspecto especial da Olimpíada é sua natureza colaborativa, na qual as equipes trabalham juntas para resolver problemas, diz Yin. Ele estava particularmente orgulhoso de como ele e seus colegas de equipe colaboraram em um quebra -cabeça chamado nações (abaixo). Depois que ele argumentou que uma solução oferecida por um dos membros de seu grupo deve estar errada e surgiu com uma alternativa que se mostrou correta, esse companheiro de equipe “continuou me dizendo o quão afortunado ele deveria me ter em seu time”, diz Yin. “Ter essas pessoas incríveis para trabalhar na lógica – é algo que une nosso grupo de amigos.”
Aqui estão alguns quebra -cabeças com curadoria da competição que você pode experimentar com um grupo de amigos. Alguns dos quebra -cabeças foram editados para se adequar melhor ao formato deste artigo.
Amigos
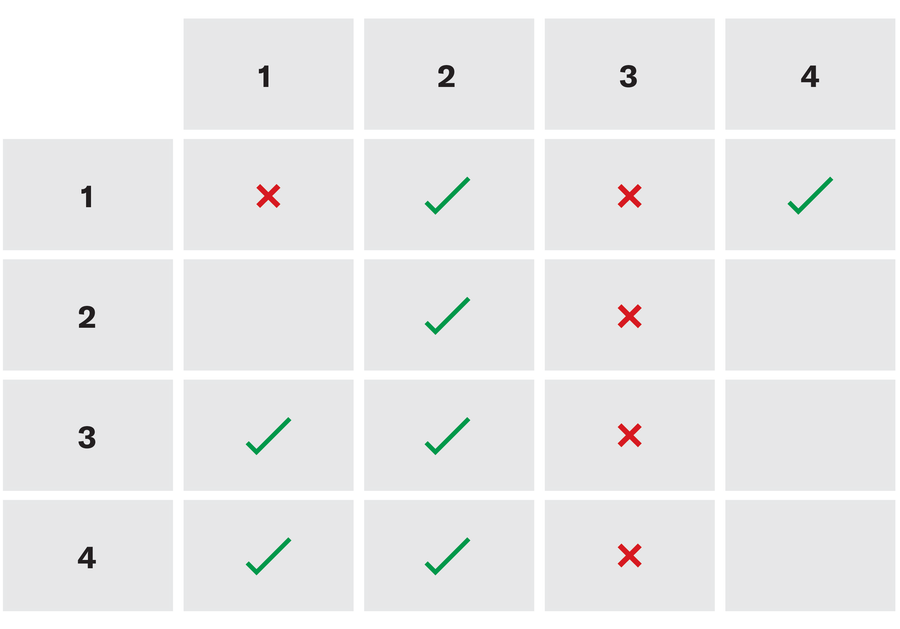
Quatro estudantes, numerados 1, 2, 3 e 4, votam entre si para determinar quem deve liderar sua sessão de revisão. Cada aluno é obrigado a votar “sim” ou “não” para cada pessoa do grupo, incluindo a si mesma. A seguir, são apresentadas declarações verdadeiras sobre suas cédulas:

Na tabela acima, as declarações do problema original da OIT na linguagem da lógica matemática estão à direita. Nossas traduções dessas declarações estão à esquerda.
Determine, na medida do possível dessas declarações, que o fizeram e não votaram em quem. Preencha isso na grade a seguir com um cheque para um voto de sim, um “x” para um voto e um espaço em branco, se você não puder saber com certeza. Cada linha representa a votação do número listado à esquerda.
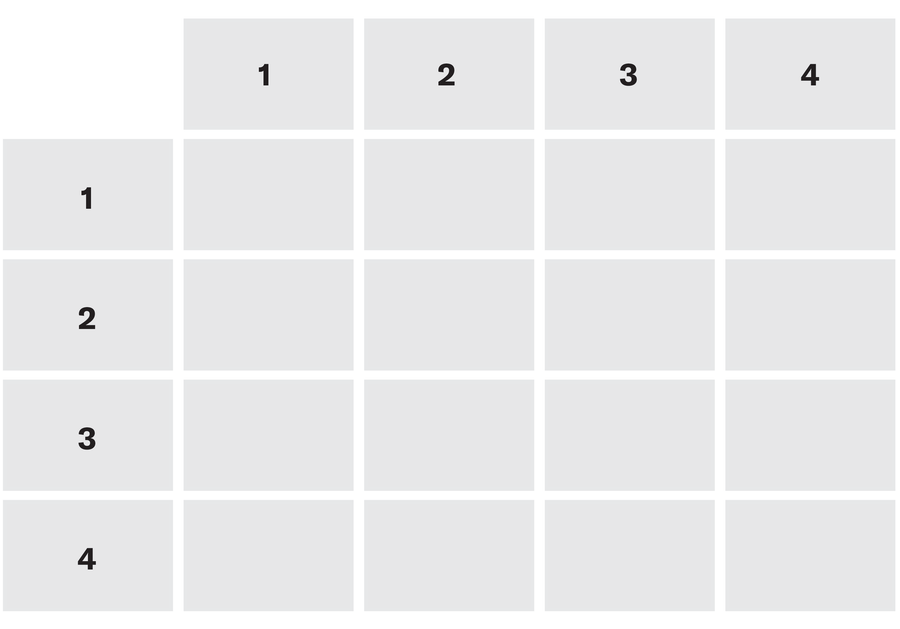
Nota: Se tivermos uma declaração UM Isso não é verdade, consideramos qualquer frase da forma “se UM, então B”Para ser verdadeiro. Por exemplo,“ Se o céu é verde, então ____ ”é verdadeiro, não importa o que seja o espaço em branco, porque a premissa é falsa. Você precisará desse fato para resolver o quebra -cabeça.
Quiz
1. Qual é a resposta para a pergunta 2?
A. b
B. a
CD
D. c
2. Qual é a resposta para a pergunta 3?
A. c
B. d
C. b
D. a
3. Qual é a resposta para a pergunta 4?
A. d
B. a
C. c
D. b
4. Qual é a resposta para a pergunta 1?
A. d
B. c
C. a
D. b
Rachaduras seguras
Uma combinação de cofre é aberta com uma série de quatro interruptores que podem ser invertidos (1) ou desligado (0). O cofre está quebrado; portanto, para abri -lo, você só precisa obter a posição de dois interruptores em particular corretos – mas não há como saber quais interruptores são os que importam. Encontre o menor conjunto de combinações que você pode tentar garantir que um deles abrirá o cofre.
Nações
Existem dois tipos de nações: forte e fraco. Somente nações fracas podem ser invadidas e apenas nações fortes podem invadir. Se uma nação forte invadir uma nação fraca, anexará a nação fraca, mas ficará fraca e, portanto, invadível, por algum período de tempo. Apenas uma nação forte pode invadir uma nação fraca de cada vez. Se várias nações decidirem invadir a mesma nação fraca, é escolhido aleatoriamente para invadir. Cada nação quer ser o maior possível, mas não às custas de ser anexado. Suponha que todas as nações sejam completamente racionais. Existem cinco nações fortes e uma nação fraca. A nação fraca será invadida?
Dica: tente começar com uma nação forte e uma nação fraca primeiro e depois se acumule a partir daí. Para resolver o problema, tente ver como os casos complexos podem ser reduzidos a mais simples e nobrek; – um método formalmente conhecido como “indução matemática”.
Sudoku Puzzle
Esse quebra -cabeça também foi incluído no OIT. Os concorrentes tiveram que resolvê -lo sob um limite de tempo usando apenas um lápis e papel.
Amigos
Quiz
1. D
2. C
3. B
4. A
Rachaduras seguras
Para garantir que você possa quebrar o cofre, você precisará ter todos os conjuntos possíveis de posições para cada par de comutadores representados. Dessa forma, não importa quais dois interruptores sejam os que importam ou quais posições abrem o cofre, um dos códigos o quebrará. O número mínimo de combinações necessárias é cinco. Aqui está uma solução possível: 1000, 0100, 0010, 0001, 1111.
Nações
Aqui está uma maneira de pensar isso. Suponha que tenhamos uma nação forte e uma nação fraca. A nação forte naturalmente deseja invadir a fraca, porque não há outra nação para invadir a forte depois que o faz. Que tal duas nações fortes e uma nação fraca? Bem, se uma das nações fortes anexasse a nação fraca, ela se tornaria temporariamente fraca e seria invadida pelo outro, para que nenhum deles gostasse de invadir em primeiro lugar, sabendo que eles seriam invadidos de volta. Agora considere três nações fortes e uma nação fraca: novamente, se uma nação forte invadir, ficamos com duas nações fortes e uma nação fraca, uma situação em que apenas determinamos que ninguém invadiria – então as três nações fortes desejariam invadir neste caso. Usando a mesma lógica, se houver quatro nações fortes e uma invadir, o cenário reduzirá o caso de três nações de três fortes em que todos gostariam de invadir, para que nenhuma das quatro nações arriscaria invadir em primeiro lugar. Finalmente, isso nos leva a cinco nações fortes e uma nação fraca, um cenário em que todas as nações fortes desejam invadir porque, uma vez que haja quatro nações fortes e uma que se tornou fraca de anexar, ninguém invadirá.



